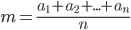Sommes et inégalités

Les fonctions logarithme et exponentielle permettent d'établir certaines inégalités qu'il est difficile d'obtenir autrement. L'idée est d'appliquer plusieurs fois l'une des deux propriétés suivantes :

- pour tout réel x > 0, ln(x) ≤ x - 1

- pour tout réel x, e^x ≥ 1 + x

Comparaison de moyennes

On considère les nombres réels strictement positifs a₁, a₂, ..., a_n, avec n ≥ 2.

On définit leur moyenne arithmétique m, leur moyenne géométrique g et leur moyenne harmonique h par les relations :

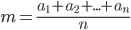$m=\frac{a_1+a_2+...+a_n} n$ , $g=\sqrt[n]{a_1a_2...a_n}$ et $\frac 1 h = \frac 1 n \left(\frac 1 a_1+\frac 1 a_2 + ... + \frac 1 a_n \right)$ .

On se propose de démontrer que $h\leq g\leq m$ .

Le cas n = 2 peut être résolu assez simplement, mais la généralisation n'est pas aisée.

Appliquons la relation ln(x) ≤ x - 1 aux réels $\frac {a_1} m$ , $\frac {a_2} m$ , ..., $\frac {a_n} m$ . On obtient :

$\text{ln}\left( \frac{a_1} m \right) \leq \frac{a_1} m - 1$ , puis $\text{ln}\left( \frac{a_2} m \right) \leq \frac{a_2} m - 1$ , ..., $\text{ln}\left( \frac{a_n} m \right) \leq \frac{a_n} m - 1$ .

En ajoutant membre à membre ces n inégalités on obtient :

$\text{ln}\left(\frac{a_1}{m}\right)+\text{ln}\left(\frac{a_2}{m}\right)+...+\text{ln}\left(\frac{a_n}{m}\right) \leq \frac{a_1}{m}-1+\frac{a_2}{m}-1 + ... +\frac{a_n}{m}-1$

soit $\text{ln}\left(\frac{a_1a_2...a_n}{m^n}\right) \leq \frac{a_1+a_2+...+a_n}{m}-n$ .

Or a₁+a₂+...+a_n = nm, on a donc $\text{ln}\left(\frac{a_1a_2...a_n}{m^n}\right) \leq 0$ .

On en déduit que $\frac{a_1a_2...a_n}{m^n} \leq 1$ , d'où $a_1a_2...a_n \leq m^n$ et finalement $\sqrt[n]{a_1a_2...a_n} \leq m$

d'où g ≤ m.

Pour montrer que h ≤ g, on applique le résultat précédent aux réels strictements positifs s 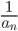$\frac 1 {a_1}$ , $\frac 1 {a_2}$ , ..., $\frac 1 {a_n}$ . On obtient immédiatement 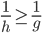$\frac 1 h \geq \frac 1 g$ , donc h ≤ g.

Problème

1) a₁, a₂, ..., a_n sont des nombres réels dont la somme est égale à 0, c'est à dire tels que

a₁+ a₂+ ...+ a_n= 0. Montrer que 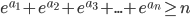$e^{a_1}+e^{a_2}+e^{a_3}+ ... + e^{a_n} \geq n$

2) b₁, b₂, ..., b_n sont des réels positifs. Montrer que $\frac {b_1} {b_2}+\frac {b_2} {b_3}+\frac {b_3} {b_4}+ ... +\frac {b_{n-1}}{b_n} + \frac {b_n} {b_1} \geq n$ .

3) c₁, c₂, ..., c_n sont des réels positifs. Montrer que $c_1+c_2+c_3+ ... +c_n +\frac {1} {c_1 c_2 c_3 ... c_n} \geq n+1$ .