Sommes d'entiers
Quelle est la somme des entiers de 1 à n ? Quelle est la somme de leurs carrés ou celle de leurs cubes ? Il existe des formules, classiques, permettant d'effectuer rapidement ces calculs et on peut les retrouver à l'aide de petits dessins à interpréter correctement. Voici quelques exemples de ces dessins suivis d'un problème à résoudre.
Somme des entiers naturels de 1 à n
ou
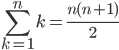
Preuves sans mots
 ou
ou
Somme des premiers nombres impairs
ou

Preuve sans mots

Somme des carrés des entiers naturels de 1 à n
ou
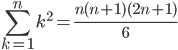
Preuves sans mots
 ou
ou 
Somme des cubes des entiers naturels de 1 à n
ou
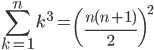
Preuves sans mots
 ou
ou
Problème
On écrit la suite des nombres impairs pour former un triangle comme ci-dessous :
|
1 |
|
|
|
|
|
1 |
|
3 |
5 |
|
|
|
|
8 |
|
7 |
9 |
11 |
|
|
|
27 |
|
13 |
15 |
17 |
19 |
|
|
64 |
|
21 |
23 |
25 |
27 |
29 |
|
125 |
On calcule la somme des termes écrits sur chaque ligne et on voit apparaître une propriété.
Enoncer cette propriété et la démontrer.
Sources et compléments :
1 - Les "preuves sans mots" sont tirées du livre "Proofs without words" de Roger B. Nelsen. On peut en lire des extraits sur Google-Livres.
2 - Voir l'article Wikipédia Somme (arithmétique)