

D'après Wikipédia, le pointillisme est une technique de peinture impressionniste qui consiste à peindre par juxtaposition de petites "taches" de peinture.
L'idée d'associer une couleur à chaque point du plan est à la base du problème suivant.
A chaque point du plan on associe l'une des deux couleurs : rouge ou bleu. Démontrer qu'il existe au moins un triangle équilatéral dont les trois sommets ont même couleur.
Il s'agit donc de déterminer une configuration dans laquelle un triangle équilatéral a nécessairement ses 3 sommets de même couleur. Pour cela considérons le réseau de triangles équilatéraux dessinés ci-dessous.
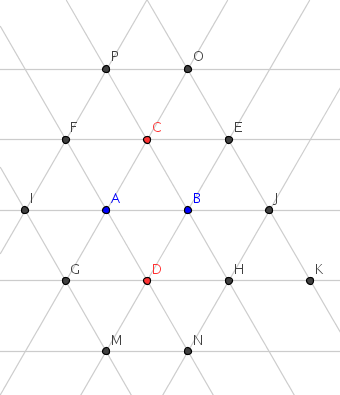 Nous allons colorer les sommets en essayant d'éviter à chaque étape qu'un triangle équilatéral ait ses trois sommets de même couleur.
Nous allons colorer les sommets en essayant d'éviter à chaque étape qu'un triangle équilatéral ait ses trois sommets de même couleur.
Comme chaque triangle équilatéral aura toujours deux sommets de même couleur, commençons par colorer les points A et B en bleu.
Les points C et D sont les sommets des triangles équilatéraux ABC et ABD, ils doivent être colorés en rouge.
Les points I et J sont des sommets des triangles équilatéraux CDI et CDJ qui ont déjà deux sommets rouges, ils doivent donc être colorés en bleu.
Les points E et F sont des sommets des triangles équilatéraux AFI et BEJ qui ont déjà deux sommets bleus, ils doivent donc être colorés en rouges.
On constate alors que le triangle DEF a trois sommets rouges. Il n'est donc pas possible de faire en sorte qu'aucun triangle équilatéral n'ait ses trois sommets de même couleur.
A chaque point du plan on associe l'une des deux couleurs : rouge ou bleu.
Démontrer qu'il existe au moins un rectangle dont les quatre sommets ont même couleur.