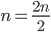La moitié du double

Pour calculer un nombre il suffit de trouver la moitié de son double. Voilà bien une idée de mathématicien qui semble incapable de résister au plaisir de faire compliqué quand on peut faire simple.

Un premier exemple

Par exemple, pour compter le nombre de personnes présentes dans une pièce, on peut compter le nombre de jambes, puis diviser par 2 et illustrer ainsi la jolie formule 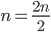$n=\frac {2n} 2$ . Ces n personnes se sont toutes serré la main à leur arrivée. Combien de poignées de mains cela fait-il ?

Essayons d'abord de faire simple en calculant directement le nombre de poignées de mains. Considérons chacune des n personnes :

- la 1ère a serré les mains de toutes les autres personnes, donc n-1 mains;

- la 2ème a serré la main de la 1ère personne, mais cette poignée de mains a déjà été comptée, et ensuite les mains des n-2 autres personnes.

- la 3ème personne a serré les mains des 2 premières, mais ces poignées de mains ont déjà été comptées, et ensuite les mains des n-3 autres personnes.

- on peut continuer ainsi jusqu'à la dernière personne à qui tous les autres ont déjà serré la main et qui n'engendre donc pas de poignée de mains supplémentaires.

Au total, le nombre de poignées de mains échangées est donc :

P_n = (n-1) + (n-2) + (n-3) + ... + 2 + 1 + 0

c'est à dire la somme de tous les entiers de 0 à n-1. C'est simple, mais pas très pratique à calculer lorsque n devient grand.

Tournons nous à présent vers la façon compliquée de voir les choses et cherchons d'abord le double du nombre de poignées de mains.

Chacune des n personnes a serré la main de n-1 personnes : cela fait n(n-1) poignées de mains, mais comme chaque poignée de mains concerne deux personnes, ce résultat est le double du nombre total de poignées de mains. Il nous reste donc à diviser par 2 pour trouver le nombre de poignées de mains qui est alors :

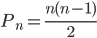$P_n=\frac{n(n-1)} 2$ .

La formule obtenue est beaucoup plus pratique à utiliser que la précédente.

On notera au passage que le fait d'avoir calculé P_n de deux façons différentes nous fournit la démonstration de la formule :

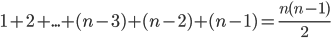
$1+2+...+(n-3)+(n-2)+(n-1) = \frac{n(n-1)} 2$

La somme des entiers de 1 à n-1 est égale à $\frac{n(n-1)} 2$ .

En géométrie aussi ...

Nous venons de voir, à propos du problème des poignées de mains, comment l'idée a priori saugrenue de prendre la moitié du double peut se révéler efficace. Il ne s'agit pas du tout d'un cas isolé; la géométrie élémentaire et les calculs d'aires vont nous fournir d'autres exemples.

Comment calculer l'aire d'un triangle rectangle dont les côtés de l'angle droit ont pour mesures a et b ?

La méthode est simple : on cherche l'aire double en utilisant un second triangle identique au premier et en le plaçant à côté du premier pour former un rectangle de dimensions a et b. Le double de l'aire du triangle rectangle est donc le produit a⤫b, ce qui nous permet de dire que l'aire du triangle rectangle est 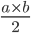$\frac{a \times b} 2$ .

De la même façon on trouve l'aire d'un triangle quelconque ou l'aire d'un trapèze en calculant leur double qui est l'aire d'un parallélogramme.

On trouve ainsi que l'aire d'un triangle de base b et de hauteur h est $\frac {b \times h} 2$ .

Et pour un trapèze de grande base B, de petite base b et de hauteur h, l'aire est tout naturellement 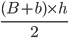$\frac {(B+b) \times h} 2$ .

Problème

ABC est un triangle équilatéral à l'intérieur duquel se trouve un point M tel que AM=3, BM=4 et CM=5.

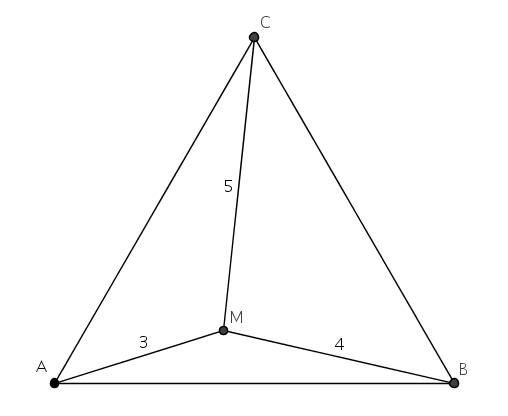
Calculer l'aire de ABC.