Irrationalité du nombre e


e est le nombre réel tel que ln  e=1. 


Le but du problème est de montrer que e n'est pas un nombre rationnel, c'est-à-dire qu'il ne peut pas s'écrire sous la forme \frac p q avec p et q entiers.


Pour tout entier n>0, on pose In = 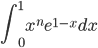\int_{0}^{1} x^ne^{1-x}dx .

1) A l'aide d'une intégration par parties, calculer l'intégrale I1 = \int_{0}^{1} xe^{1-x}dx  

2.a) Montrer que pour tout x de [0;1]: xn ≤ xne1-x ≤ exn.

2.b) Exprimer en fonction de l'entier n l'intégrale Jn = 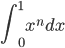\int_{0}^{1} x^ndx.

2.c) En déduire que pour tout n>0, 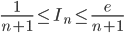\frac 1 {n+1} \leq I_n \leq \frac e {n+1}.

3) Montrer que, pour tout n>0, on a In+1 = (n+1) In - 1.

4) Pour tout entier n>0 on pose kn = n!e - In.

4.a) Exprimer kn+1 en fonction de kn .

4.b) Calculer k1 .

4.c) En déduire, à l'aide d'un raisonnement par récurrence sur n que kn est un nombre entier pour tout n strictement positif.

4.d) Montrer que : pour tout n>1, le nombre n!e = kn + In n'est pas un nombre entier.

5) Soient p et q deux entiers strictement positifs. 

5.a) Montrer que pour n ≥ q,  \frac {n!p} q est un nombre entier.

5.b) En déduire que e n'est pas un nombre rationnel (on pourra raisonner par l'absurde ).