Problèmes de recherche Problèmes de recherche
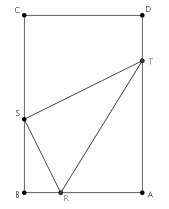Soit ABCD une feuille rectangulaire de largeur AB=4 et de longueur BC=6.
Soit R un point de [AB] (bord inférieur de la feuille) et T un point de [AD]
(bord droit de la feuille). On replie la feuille suivant [RT] et on appelle S la
nouvelle position du point A (coin inférieur droit de la feuille).
Dans tout l'exercice, on s'intéresse au cas où S est sur le segment [BC] (bord gauche de la feuille).
On pose AR=`x` et AT=`y`.
1- Trouver les valeurs minimales et maximales de `x`.
2- Trouver une relation entre `x` et `y` lorsque S se déplace sur [BC].
3- Trouver la valeur de `x` pour laquelle la partie repliée (triangle RST)
est minimale. Quelle est alors la nature du triangle AST ?
Une pompe A met 15 mn de plus qu'une pompe B pour vider un bassin. Les deux pompes fonctionnant simultanément réalisent l'opération en 56 mn.
Quel temps faut-il à chacune des deux pompes pour vider le bassin ?
Quelles sont les fonctions affines `f` telles que pour tout réel `x`, `f@f(x)=4x-3` ?
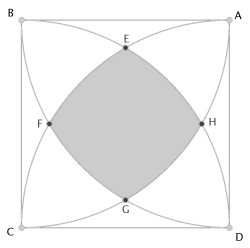
Un vitrail est formé d'un carré ABCD de côté a et de quatre quarts de cercle centrés respectivement aux sommets du carré et de rayon a comme l'indique la figure. La partie centrale est un quadrilatère curviligne EFGH.
Déterminer l'aire de ce quadrilatère curviligne en fonction de a.
On considère la suite `(u_n)` définie par `u_n = n^5 - n`.
Démontrer que tous les termes de cette suite sont des multiples de 10.
Calculer le produit `A = (1-4/1^2)(1-4/2^2)(1-4/3^2)...(1-4/199^2)`.